Mel Bartels affirme que les miroirs en ménisques sont plus rigides que les miroirs concaves pour une épaisseur de verre égale au bord.
J'ai calculé la déformée de miroirs plans, concaves et en ménisques avec un code de calculs aux éléments finis, et avec PLOP.
Je montre qu'un miroir mince en ménisque, ouvert à 3, se comporte exactement comme un miroir plan de même épaisseur. Il se déforme effectivement moins qu'un miroir concave de même épaisseur au bord comme le dit Mel Bartels. Enfin je montre que PLOP peut très bien calculer les déformations des ménisques en lui faisant calculer un verre quasi plan.
Présentation du problème
Mel Bartels affirme que les miroirs en ménisques sont plus rigides que les miroirs concaves.
Le miroir en ménisque de Mel Bartels. Image de Mel Bartels adaptée.
Dans un article d'avril 2011 sur son site Internet, le très innovant astronome amateur américain Mel Bartels affirme qu'un miroir très ouvert et en forme de ménisque est plus résistant aux déformations qu'un miroir moins ouvert et de forme concave conventionnelle.
L'astronome américain Mel Bartels a publié (début avril 2011)
( bbastrodesigns.com/tm.html
)
plusieurs articles sur son dernier miroir taillé dans une pièce de verre en forme de ménisque
( bbastrodesigns.com/ JoyOfMirrorMaking/Intro.html
et
bbastrodesigns.com/ ZipDob/ZipDob.html
).
Le miroir en question est en verre à vitre, mesure 340 mm de diamètre pour 25 mm d'épaisseur et est ouvert à 3,0.
C'est donc un miroir très ouvert puisqu'à ce jour les amateurs ne descendent guère en dessous d'une ouverture de 4,0.
De plus Mel Bartels le supporte sur un barillet à seulement trois points (dont il ne précise pas l'écartement).
Ce qui est fort peu compte tenu du rapport diamètre épaisseur du verre.
Enfin il affirme que la figure de diffraction est très propre.
Formes d'un verre concave et en ménisque de même épaisseur au bord
Si j'ai bien compris, dans le fil du texte, Mel Bartels affirme que les miroirs à très forte ouverture sont plus résistants à la flexion du fait de leur forme sphérique prononcée. Un miroir de très longue focale serait moins résistant du seul fait que sa forme s'approche plus d'un disque totalement plat comme une feuille de papier. Tandis qu'un miroir de forme très sphérique et très mince serait, du seul fait de son relief, bien plus résistant aux flexions, à l'image d'une feuille de papier pliée. Il explique aussi que la forme en ménisque réduit l'épaisseur et la masse du verre, ce qui limite les efforts et donc les déformations.
En résumé, Mel Bartels considère qu'un miroir en forme de ménisque résiste mieux aux déformations du fait du moment d'inertie lié à sa courbure et du fait de la réduction de masse apportée par la forme sphérique du dos du miroir.
Cet justification me semble voisine d'une autre argumentation de Mel Bartels, introduite dans la description de son télescope 'trilatéral' plusieurs années avant. Il y affirmait que le calage latéral d'un miroir devait être réalisée préférentiellement par des cales à 90° (et non pas à 120° comme il est plus usuel et plus historique). Son argumentation posait que les efforts orthogonaux de pliure se contrecarraient et qu'il en résultait moins de flexions dans une forme sphérique. Notez bien que j'ai adhéré à ces affirmations sans les critiquer ni chercher à les vérifier, tant elles me semblaient intuitives. Je les ai reprise à mon compte parmi les justifications du calage à 90° du miroir de mon télescope de voyage.
Or, même en ménisques, nos miroirs sont essentiellement plats et de faibles moments d'inertie.
Fenêtres du logiciel PLOP: Modèle de calcul et carte de déformation d'un miroir
Les affirmations de Mel Bartels sont très surprenantes: Son miroir de 340 mm de diamètre épais de 25 mm, qui plus est en verre à vitre tout à la fois plus lourd -de 10%- et plus souple -de 5%- que le verre borosilicate, donnerait de bonnes images tout en étant porté par seulement trois points d'appuis ! ? Sachant que mon miroir de 250 mm épais de 27 mm est porté sur 9 points et que l'on supporte volontiers un disque de 400 mm épais de 40 mm avec 18 points, il y a de quoi s'interroger. J'ai donc souhaité vérifier et critiquer ces affirmations.
Dans le monde des amateurs, on dispose du code de calcul PLOP de M. David Lewis
( davidlewistoronto.com/plop
).
Ce logiciel calcule les déformations mécaniques d'un disque de verre à dos plat et à face optique concave.
Il sait aussi analyser les déformations mécaniques pour déduire les effets optiques sur l'image.
En particulier il détermine la déformation résiduelle après mise au point.
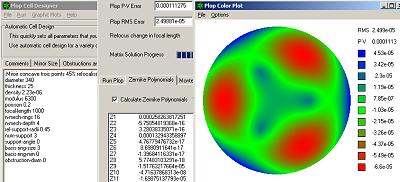
Pour fixer les ordres de grandeurs, j'ai calculé avec PLOP le miroir aux caractéristiques suivantes que l'on retrouve sur l'illustration ci-jointe:
- Diamètre 340 mm par 34 mm d'épaisseur au bord
- Disque de verre à vitre de densité 2,45e-06 kg/mm³ , module d'élasticité 6000 kgF/mm² et coefficient de Poisson 0,22
- Les miroirs concaves ou ménisques ont une focale est 1000 mm (F/D= 2,94 et R= 2000 mm).
- Le maillage de calcul est de 16x4. C'est-à-dire que le rayon est découpé en 16 et l'épaisseur du verre en 4
- Supporté par trois points à 43% du rayon (car cela minimise la déformation optique résiduelle)
PLOP calcule une déformation optique résiduelle après mise au point de 62 nanomètres crête-à-creux sur le verre. Soit 62 nm Pic-Vallée sur le verre, ou encore Lambda sur 4 en pic-vallée sur l'onde. L'illustration ci-contre présente les fenêtres de calculs de PLOP pour ce miroir. On retrouve sur la légende de la carte des déformations résiduelles les valeurs P-V de 6,198e-05 mm ou 62 nm (et RMS de 1,412e-05 mm ou 14 nm pour l'écart type des déformations.
Cette déformation résiduelle est juste la borne supérieur des déformations acceptées par les amateurs. Il ne faudrait donc pas que le verre soit plus mince ni plus souple. Voir, il serait mieux d'avoir moins de déformations... Le miroir de Mel Bartels qui est plus mince de 9 mm est donc bien surprenant.
Pour analyser cela, il faut calculer la déformée du ménisque avec un code de calculs aux éléments finis.
Les affirmations de Mel Bartels pointent sur les spécificités des ménisques tant pour les calculs de l'inertie que de la masse. Comme PLOP ne traite que les disques à dos plat et à face concave, il faut un autre outil de calcul.
J'ai bien imaginé de donner une focale très grande à PLOP. La concavité est alors négligeable. Le résultat de PLOP est alors celui d'un disque plan de même épaisseur en tout point. Le fait que le verre soit de la même épaisseur partout ressemble à la configuration du ménisque. Mais les déformations du ménisque peuvent-elles être approchées par un calcul à plat ? Si je comprends bien Mel Bartels, il y aurait une spécificité à la forme en ménisque. On ne peut donc pas faire l'impasse a priori sur une modélisation précise de la géométrie en ménisque.
PLOP n'est donc pas utilisable pour analyser complètement ce problème. Ou alors, il faut commencer par montrer qu'il n'y a pas de différence entre les déformations d'un disque plan et d'un disque en ménisque.
Démarche d'étude adoptée
J'ai pris un code de calcul aux éléments finis réputé
Le logo du code de calcul COMSOL
J'ai trouvé un camarade dans un bureau d'étude disposant du logiciel COMSOL et partageant mon envie de faire ces calculs.
COMSOL est un produit de la société: COMSOL
( comsol.com
ou
comsol.fr
).
La version 3.2 dont nous avons pu disposer quelques heures date de 2005. La version 3.3 de 2007 coutait déjà 8000 € par an! ... et la version de fin 2010 est déjà la 4.0.
Sur le papier l'outil est sur dimensionné puisqu'il est capable de résoudre des problèmes complexes à physiques multiples. Nous ne l'avons utilisé que pour calculer des contraintes et des déformations de solides statiques 3D avec des équations linéaires.
Notre modeste version 3.2 a tourné sur un PC Windows XP en 32 bits avec seulement 1Go de mémoire. Cette limitation de la machine, couplé à nos manques d'entrainement, sont sans doute la cause de plusieurs de nos insuccès, en particulier pour les maillages trop détaillés... Mais ces difficultés nous semblent avoir été contournées avec un ratio précision de résultat sur investissement raisonnable.
Le code COMSOL permet de définir la géométrie du volume du miroir par des plans et des sphères. La différence entre sphère et parabole étant de quelques microns, l'approximation en sphère des faces semble raisonnable. Il permet aussi de fixer les points du barillet arrière à trois appuis et du barillet latéral à deux appuis que l'on utilise lorsque le miroir ne pointe plus seulement au zénith, par exemple sur la Polaire.
J'ai créé des modèles de miroirs plans, concaves et en ménisques.
Le ménisque avec barillet à 3 points et 2 supports latéraux
Les miroirs font 340 mm de diamètres et de 25 mm au bord. Les plans et ménisques ont donc 25 mm partout. Tandis que le concave ne fait plus que 19 mm au centre du fait de sa focale de 1000 mm. On peut suspecter que le centre du miroir concave sera moins rigide...
Tous les calculs ont été menés avec des paramètres communs:
- Diamètre du miroir de 340 mm épais de 25 mm au bord (sauf précision contraire)
- Verre borosilicate type Duran 50: densité 2230 kg/m³ , module d'élasticité 63E9 Pa et coefficient de Poisson 0,20
- Faces planes ou de 2000 mm de rayon de courbure ( focale de 1000 mm et ouverture à 2,94)
- Support à trois points sur un rayon de 40% pour les plans et ménisques, et 45% pour les concaves)
- Support à deux points en périphérie espacés de 90° lorsque le miroir ne pointe pas au zénith.
- Miroir orienté au zénith ou à 45° (l'étoile Polaire sous nos latitudes) dans une gravitation de 9,81 m/s².
La position en hauteur des appuis latéraux n'a pas été déterminée avec précision. Elle correspond approximativement à la hauteur du centre de gravité du verre.
L'étape suivante de la modélisation est de définir les déplacements possibles des points d'appuis et l'orientation de la gravité. Ici les appuis sont fixes et la gravité est normale au plan du verre au zénith et à 45° pour la Polaire.
Enfin, on détermine le maillage. Malheureusement, nous n'avons pas trouvé comment figer dans COMSOL un unique maillage pour tous les cas étudiés, ni comment réaliser un maillage de géométrie cylindrique simple et de bon goût pour notre disque bêtement rond... Mystère de la communication entre un machin hyper-informatisé et un utilisateur bassement-humain... Les maillages sont donc tous différents et fort peu satisfaisants. On s'est juste arrangé pour disposer de plus de 2000 points de calculs par face et plusieurs couches de points dans l'épaisseur du verre. Ce qui fait des maillages plus fin que le centimètre a priori...
J'ai développé une interface pour déduire les déformations optiques à partir des résultats du code.
On trouve sur Internet diverses comparaisons des résultats de COMSOL et de PLOP. C'est un bon signe! Sauf qu'il faut être grand clerc pour transformer les résultats bruts de COMSOL exprimés en déplacements nanométriques sur un maillage en une trentaine d'intégrales rigoureuses sur la surface optique... Il a donc fallu réaliser cette transformation avec un bout de calcul Excel. Ainsi les résultats sont finalement exprimés en déformations pic-vallée du verre et en polynômes de Zernike comme il est d'usage pour interpréter les déformations optiques. La précision de la conversion n'est toutefois pas entièrement satisfaisante et justifiera de revenir sur ces calculs un jour... peut-être...
Les deux dernières difficultés de méthodes ont été de vérifier la précision-reproductibilité des résultats et de comprendre pourquoi PLOP ne normalilse pas ses polynômes comme moi...
Pour les polynômes de Zernike, j'utilise les notations du professeur James C. Wyant (Optical Sciences Center, University of Arizona). Ces notations présentent avantageusement les résultats en hauteur maximale de déformation du verre. Mais manifestement PLOP n'a pas les mêmes notations puisque ses résultats diffèrent d'un coefficient variable pour chacun des polynômes. Après investigation, PLOP donne ses résultats en écart type de la déformation du verre. Ce qui est commode pour déterminer l'écart type des déformations totales (ou écart RMS) d'une simple somme quadratique des coefficients. C'est une autre approche... mais du coup il faut convertir les valeurs PLOP pour les comparer aux déformations calculées avec COMSOL.
Les résultats COMSOL présentent des curiosités. Par exemple, alors que le problème est symétrique, la surface calculée est légèrement penchée (on parle de 'tilt'). Et encore, tandis que la symétrie est d'ordre 3 (on est sur trois points), la surface présente des déformations en pliure (ordre 2 et 4 des astigmatismes et comas)... Toutefois ces anachronismes sont de faibles amplitudes: entre 1 et 10 nm à comparer aux autres déformations 10 à 100 fois plus fortes. L'origine de ces valeurs curieusement non nulles a été analysée: C'est clairement l'effet du maillage COMSOL non régulier qui est difficilement convertible en pas d'intégration régulier. Il faudrait une mathématique bien plus compliquée pour passer de l'un à l'autre... Il faut donc considérer que, en l'état de notre maîtrise de COMSOL, certains résultats sont à considérer comme nul car non physique et que les autres sont entachés d'une erreur de 1 à 10 nm selon l'ordre de grandeur...disons 10%!
J'ai commencé prudemment par comparer mes résultats avec ceux de PLOP.
| Cas de simulation | ||||
|---|---|---|---|---|
| Code | PLOP | COMSOL | ||
| Forme | Concave | Plan | Concave | Plan |
| Support | 45% | 40% | 45% | 40% |
| Orientation | Zénith | Zénith | Zénith | Zénith |
| Coefficients de Zernike en nanomètres de verre | ||||
| Piston | -258 | -170 | -224 | -175 |
| 'tilt' | 0 | 0 | 9 | 7 |
| Mise au point | -230 | -152 | -221 | -140 |
| Astigmatisme | 0 | 0 | 4 | 0 |
| Coma | 0 | 0 | 1 | 1 |
| Sphéricité | 34 | 23 | 33 | 21 |
| Trifeuille | 49 | 26 | 41 | 23 |
| Pic-Vallée sur le verre en nanomètres | ||||
| Sans mise au point | 490 | 319 | 470 | 299 |
| Avec mise au point | 111 | 65 | 117 | 63 |
Vérification de la méthode sur des cas
calculables avec PLOP et avec COMSOL
Dans les calculs PLOP j'ai recherché la position optimale des trois points d'appuis du barillet pour minimiser la déformation optique une fois l'image mise au point. J'ai ensuite utilisé cette position dans COMSOL.
Il faut noter qu'il y a peut-être une différence résiduelle entre PLOP et COMSOL dans les coefficients d'élasticités. PLOP utilise le 'kilogramme force' dont la conversion en unités internationales n'est pas sans ambiguïté... Pour imposer à PLOP de calculer un miroir plan, je lui impose une focale de 100 mètres. Ce qui est très raisonnablement équivalent à un plan puisque la concavité d'un tel verre n'est que de 70 microns.
PLOP et COMSOL donnent des résultats raisonnablement équivalents pour un miroir plan et un miroir concave pointant au zénith. Ce qui valide les modèles, notre manière de mettre en œuvre COMSOL et notre façon de traiter les résultats.
Sur le tableau donnant les résultats ci-contre, pour ne pas surcharger, on n'a pas indiqué les angles des déformations orientées: 'tilt', astigmatisme, coma, tri-feuille; mais seulement leur intensité. On constate pour les écarts significatifs (pour le type de déformation induite par le support à trois point: La mise au point, la sphéricité et le tri-feuille) que les valeurs sont semblables. Aux écarts prêts pouvant être attribués à la conversion des déformations mécaniques en déformations optiques, à la qualité du maillage,... Cette qualité de ressemblance des résultats décomposés en polynômes de Zernike se retrouve dans les écarts pic-vallée totaux avec et sans mise au point.
Sur les sorties graphiques ci-contre, les résultats de PLOP et de COMSOL sont comparables, même si les codages de couleurs ne sont pas identiques. On parle bien d'une grosse dé-focalisation avant le calcul de la meilleure mise au point. Tandis qu'une fois la mise au point faite, il reste une aberration de sphéricité et un tri-feuille induit par les trois points d'appuis au dos du verre. Les mini maxi de ces graphiques se retrouvent dans le tableau.
Les résultats de COMSOL pour le même miroir avec mise au point (à drt) et sans mise au point (à gch)
Le modèle PLOP (à gch) et le résultat graphique PLOP (à drt) pour un miroir concave avec mise au point
Enfin j'ai calculé les déformations de divers miroirs dans diverses orientations.
| Cas de simulation | ||||||
|---|---|---|---|---|---|---|
| Forme | Concave | Ménisque | Plan | Concave | Ménisque | Plan |
| Support | 45% | 40% | 40% | 45% | 40% | 40% |
| Orientation | Zénith | Polaire | ||||
| Coefficients de Zernike en nanomètres de verre | ||||||
| Piston | -224 | -159 | -175 | -137 | -111 | -124 |
| 'tilt' | 9 | 5 | 7 | 11 | 5 | 18 |
| Mise au point | -221 | -141 | -140 | -158 | -97 | -99 |
| Astigmatisme | 4 | 1 | 0 | 6 | 2 | 0 |
| Coma | 1 | 2 | 1 | 3 | 1 | 1 |
| Sphéricité | 33 | 21 | 21 | 20 | 14 | 14 |
| Trifeuille | 41 | 22 | 23 | 21 | 12 | 15 |
| Pic-Vallée sur le verre en nanomètres | ||||||
| Sans mise au point | 470 | 300 | 299 | 342 | 206 | 225 |
| Avec mise au point | 117 | 66 | 63 | 85 | 42 | 46 |
Calculs des miroirs avec COMSOL
Avec COMSOL, nous avons calculé les déformations des verres concaves, en ménisques et plans selon deux orientations: Vers le zénith et vers la Polaire. Puis j'ai transformé les résultats en déformations optiques. Voir le tableau de résultats
Le calcul sur la Polaire se justifie par l'affirmation de Mel Bartels selon qui la qualité de l'image sur étoile est bonne. Compte tenu du mouvement des étoiles, de la nécessité de grossir et du temps d'analyse nécessaire, c'est préférentiellement sur cette étoile que l'on teste un télescope. Il eu été encore mieux de tenir compte de l'obstruction du miroir secondaire qui masque les défauts du centre du verre...
On constate des valeurs d'astigmatisme et de coma faibles et peut-être inférieures à la précision des calculs de conversion. Mais l'astigmatisme semble plus marqué sur le miroir concave tout de même.
On constate un réduction d'un facteur 1,4 entre tous les résultats au zénith et ceux sur la polaire. C'est tout à fait ce qui est attendu puisque la pesanteur est réduite d'un facteur racine de 2 ou 1,41 entre ces deux positions.
On ne prend en considération pour les conclusions de cette étude que les résultats sur la mise au point, l'aberration de sphéricité, le tri-feuille et les pics-vallées. Les résultats de coma et d'astigmatiqme sont sans-doute inférieures à la précision de calculs. De même les résultats de 'tilt' et de piston sont sans doute très influencés par les petites dissymétries des maillages et les précisions d'intégration. Ces deux derniers paramètres ne sont d'ailleurs pas des défauts optiques gênants pour l'amateur puisqu'ils sont corrigés par la collimation.
Résultats obtenus
Un miroir en ménisque se comporte exactement comme un miroir plan de même épaisseur.
Les déformations optiques des miroirs en plans et en ménisque sont les mêmes dans les résultats issus du calcul.
Ce qui appuis l'a priori selon lequel, même avec des miroirs très ouverts comme ici à 3,0, la forme du ménisque est trop proche du plan pour apporter une rigidité au miroir. Le moment d'inertie du ménisque et celui du plan de même épaisseur sont encore semblables à cette ouverture.
Un miroir en ménisque se déforme effectivement moins qu'un miroir concave.
Les miroirs concaves modélisés se déforment environ 1,6 fois plus que les miroirs en ménisques.
Comme les verres ont la même épaisseur au bord, et qu'il n'y a pas d'effet de la forme ménisque, on peut attribuer cette différence à la moindre épaisseur du concave en son centre.
La différence de déformation en tri-feuille est même de 1,8 fois. Elle semble plus sensible aux miroirs concaves. Sans doute du fait que les points d'appuis sont proches du centre où le verre est plus mince.
Un calcul avec un miroir concave de même épaisseur au centre serait intéressant pour voir si l'accroissement de rigidité du centre compense les effets du sur-poids au bord...
Le facteur 1,6 trouvé est sans-doute dépendant de l''ouverture du miroir. On imagine bien qu'un miroir peu ouvert s'approche d'un plan. Ce résultat n'est donc pas extrapolable à tous les miroirs concaves, mais seulement à ceux proche d'une ouverture de 3,0. Comme c'est le cas du miroir de Mel Bartels.
PLOP peut donc calculer les déformations des ménisques: En prenant un verre quasi plan.
En donnant à PLOP une focale 100 fois plus longue que réelle, le logiciel calcule les déformations d'un miroir quasi plan, et ces déformations sont les mêmes que celle du ménisque.
Inutile donc de revenir aux complications de COMSOL, inutile de demander une nouvelle adaptation à M. Lewis, les amateurs peuvent se suffire de ce merveilleux produit.
On a même vérifié que PLOP donnait la même déformation pic-vallée (sur un plan dont on a diminué la gravité d'un facteur 1,41) que COMSOL pour un ménisque incliné de 45° sur la Polaire.
Enfin: Restons prudents, ce n'est que du calcul...
Les résultats de COMSOL pour un ménisque visant la polaire. Mise au point calculée dans COMSOL: 41 nm P-V verre. Un léger 'tilt' est bien visible entre le haut et le bas du verre.
Une fois orienté sur la Polaire, le miroir en ménisque de Mel Bartels n'a ,selon mes calculs, que 42 nanomètres de Pic-Vallée sur le verre soit lambda sur 6,6 sur l'onde. Au zénith on est plutôt à lambda sur 4,3. L'effet d'une telle déformation est plus ou moins visible sur une étoile selon l'expérience de l'observateur.
Mais tous ces calculs ne remplacent pas l'expérience de terrain. J'ai déjà dit que certaines étapes étaient peu satisfaisantes. Et aussi, si certains trouvent qu'une valeur théorique de lambda inférieur à 10 est inacceptable et dégrade l'image, Mel Bartels, quant-à lui, trouve que son image est bien bonne.
Pierre Strock - Montigny-le-Bretonneux - Ile de France - France - 15 mai 2011