Qu'est-ce ?
En octobre 2003, dans mon club d'astronomie: Magnitude 78, nous avons décidé de tailler les miroirs de nos télescopes. Nous avons commencé avec pour seuls bagages les livres qui traitent du sujet (cf [1] et [3]), quelques articles du Web, aucune expérience antérieure ni conseil, et toute notre bonne volonté.
Nous avons achevé quatre miroirs en quelques mois. Ce sont de beaux 250 mm ouvert à 5 et taillés dans du Pyrex mince de 28 mm. La conclusion qui s'impose à la fin de cette aventure est claire: Ça marche tout seul ou presque !
Dans le « presque », il y a le contrôle du miroir en cours de travail et en particulier les calculs associés à ce contrôle. Un peu de matière grise et une feuille de calcul nous ont facilité la vie.
L'objet de cette page est de mettre à disposition notre feuille de calcul pour le contrôle des miroirs.
À quoi cela sert-il ?
À calculer le « lambda » d'un miroir astronomique parabolique.
Le lambda est l'écart Pic – Vallée de l'onde réfléchie par le miroir. L'onde est déformée par les défauts du miroir. S'il n'y a pas de défaut le Pic - Vallée est nul.
C'est la partie calcul du test de la qualité des miroirs dit : test de Foucault.
On utilise le test de Foucault lors de la fabrication des miroirs pour déterminer où sont leurs défauts à retravailler.
On l'utilise pour contrôler un miroir achevé.
Références
[1] La construction du télescope d'amateur – Jean TEXEREAU – Société Astronomique de France
[2] Lunettes et télescopes – André DANJON et André COUDER – Librairie Scientifique et Technique
[3] Réalisez votre télescope – Karine et Jean-Marc LECLEIRE – Éditions Lecleire
Quelques considérations
Le principe du contrôle de Foucault pour les novices
Par "novices" on entend ceux qui ne veulent pas quitter cette page sans en savoir un peu plus. Ceux qui souhaitent utiliser pleinement cette page ont certainement déjà lu les livres cités en référence: Ce paragraphe ne leur apportera rien.
On place une source lumineuse en forme de fente près du centre de courbure du miroir. Comme la forme du miroir est très proche d'une sphère, tous les rayons qui partent du centre de la sphère se réfléchissent et reviennent au centre de la sphère. L'image réfléchie de la fente se forme donc près du centre de courbure.
L'image ne présenterait aucune aberration si le miroir était parfaitement sphérique. Mais en astronomie on utilise des miroirs paraboliques. Donc l'image de la fente présente une aberration de sphéricité: C'est-à-dire que les rayons ne reviennent pas tous au même point. Si on imagine le miroir comme une série de couronnes concentriques à l'image d'une cible, on observe qu'il y a un foyer pour chaque couronnes (ou zones) du miroir.
Le test de Foucault se pratique avec un appareil de Foucault. Il est constitué d'une source lumineuse fixe en forme de fente que l'on place près du centre de courbure du miroir. En plaçant l'œil à coté de cette fente, on peut observer l'image de la fente réfléchie par le miroir. L'appareil comporte aussi une lame de couteau qui peut venir occulter l'image de la fente revenant du miroir. Cette lame est montée sur un chariot se déplaçant le long de l'axe optique. Le déplacement est mesuré avec un vernier précis. On peut déplacer la lame et venir occulter sélectivement les images au foyer de chaque zone du miroir. Bien que l'on juge de l'occultation à l'œil, le dispositif est très précis et permet de mesurer la position des différents foyers à dix microns près.
Les aberrations dites longitudinales (écart entre le foyer d'une zone du miroir et le foyer du centre du miroir) sont mesurées pour les différentes zones du miroir (à l’aide d’un écran à zones dit écran de Couder placé devant le miroir). On compare ces mesures aux aberrations théoriques attendues que l'on sait calculer. Les différences permettent de calculer les pentes des différentes zones du miroir. On peut donc mesurer la forme du miroir.
Mise en garde sur les critères commerciaux
Les «lambda sur 4 », «lambda sur 8 » et autres « lambda sur 16 » sont très connus. Ils correspondent souvent à des verbiages commerciaux car plus le nombre écrit est grand, plus le prix du miroir est élevé… Il peut aussi être tentant de truquer ces valeurs ! Mais surtout, les lambdas ne sont qu'un des aspects de la qualité des miroirs.
La forme du front d'onde est aussi très importante, elle doit être régulière, les pentes ne doivent pas être importantes, ni en dents de scie. Or les machines industrielles de fabrication des miroirs ont très facilement le défaut de produire des surfaces zonées. Elles sont en dents de scies même avec un lambda flatteur.
Mettre les critères dans l'ordre et les utiliser avec mesure
Tout d'abord un «lambda» meilleur que « lambda sur 4 » n'a de sens que si le critère de Couder est vérifié. Les aberrations ne doivent pas s'approcher de l'unité, sinon l'image de diffraction n'a pas de sens et le critère de Rayleigh n'a plus de sens non plus.
Enfin, l'état de surface doit être à la hauteur de la précision annoncée.
Si l'on travaille la qualité d'un miroir et que l'on va au-delà du critère de Couder et de Rayleigh, c'est essentiellement le contraste des images qui se trouve amélioré. Mais le contraste dépend aussi fortement de l'état de surface du miroir à l'échelle millimétrique. Si un miroir est annoncé à lambda sur 16 et que son état de surface est mauvais, tout l'effort déployé pour l'amener à cette précision est ruiné par la diffusion due au mamelonnement et au micromamelonnement (qui passe si souvent inaperçu). Les critères flatteurs n'ont alors pas de réalité.
C'est certainement sur l'état de surface que les astronomes progresseront dans l'avenir. Mais pour cela il reste à trouver un moyen de quantifier la qualité de l'état de surface. Sans mesures point de salut...
Comment se sert-on de la feuille de calcul ?
Il faut un appareil de Foucault avec un masque de Couder à 5 zones.
Voir les exemples et explications dans le « Texereau » [1] ou le « Danjon et Couder » [2] ou sur le Web.
Il faut une source lumineuse fixe et un couteau mobile. Les calculs sont programmés uniquement pour ce cas. Avec une source et un couteau mobiles, il faut multiplier les mesures par deux avant de les saisir.
Un paramètre permet de s'affranchir du sens de montage du vernier de mesure de l'appareil de Foucault. Ça c'est un petit plus introuvable ailleurs !
Il faut avoir fait les mesures !
Il est préférable de calculer la moyenne de plusieurs séries de mesures sur un diamètre du miroir.
Attention: Un seul diamètre !
Certains font la moyenne des mesures sur deux diamètres perpendiculaires voir même sur plus. Mais alors, le résultat n'est plus un Pic – Vallée mais un début d'évaluation de défaut moyen (souvent dit RMS en anglais). Or les critères d'appréciations d'un défaut moyen (RMS) ne sont pas ceux d'un pic-vallée (PV). Ainsi, l'équivalent du critère de Rayleigh à lambda sur 4 (L/4) en PV est le critère de Maréchal de L/14 en RMS. Certes le critère RMS rend mieux compte de la dégradation des images que le critère PV. Mais le RMS n'est pas accessible à la mesure avec un appareil de Foucault...
Il faut saisir les mesures dans les cases grises de la feuille de calcul.
Saisir des valeurs dans les cellules grises. Ne pas toucher aux autres cellules !
Une valeur de la « constante pour centrer les mesures » est calculée automatiquement. Formule issue de [3].
N.B.: On peut utiliser une autre formule de calcul en modifiant la cellule « Valeur proposée ». Par exemple certains préfèrent une constante qui donne des valeurs extrêmes d'ATF symétriques.
On peut aussi définir soit même la constante en écrasant la formule de la case « Valeur retenue » par la valeur souhaitée.
Car certains préfèrent choisir la constante à la main. Chacun son truc!

Ne pas oublier d'indiquer le sens de votre vernier !
Si vos mesures augmentent lorsque le couteau s'éloigne du miroir, vous avez un vernier droit (saisir +1). Vous être une personne rigoureuse car vous avez monté votre vernier dans le même sens que dans les livres [1] et [3]. Vous êtes dans le rang, mais vous allez vous mettre le vernier dans l'œil un de ces jours!
Si vos mesures diminuent lorsque le couteau s'éloigne du miroir, vous avez un vernier inversé (saisir -1). Vous êtes une personne au sens pratique développé, car vous avez observé que tout le monde se fourre le vernier dans l'œil ! Mais votre indiscipline vous perdra.
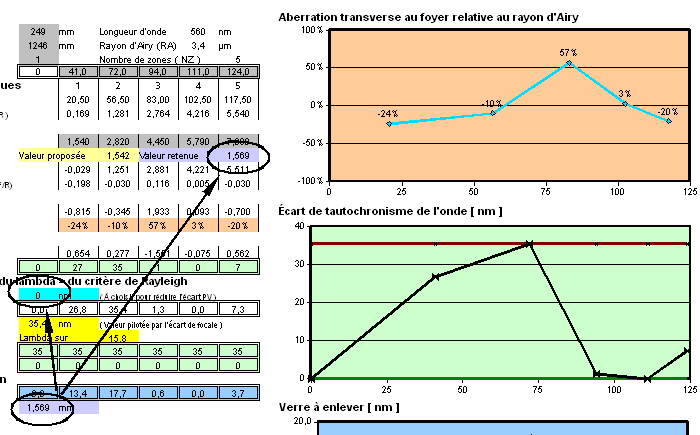
Le premier résultat permet de vérifier le critère de Couder.
Le critère de Couder stipule que les rayons doivent converger dans la tache de diffraction, sinon l'image de diffraction attendue ne se forme pas ! Ce qui se traduit par :
Chaque valeur d'aberration transverse réduite doit être inférieure à 100%.
![]()
Si le critère de Couder n'est pas respecté, la tache de diffraction n'a pas la forme théorique.

Pour les résultats suivant il faut rechercher le profil de la meilleure onde de référence.
Cette recherche se fait manuellement car on n'a pas souhaité implanter le calcul. Pour cela il faut chercher la valeur d'« Écart de focale » qui minimise la valeur d'« Écart Pic-Vallée ».

Lorsque le minimum est trouvé, sur le graphique de l'écart de totauchronisme, le profil de l'onde est encadré au plus près par deux paraboles qui représentent une meilleure onde dessus et une meilleure onde dessous.
L'une des deux meilleures ondes touche alors en deux points tandis que l'autre touche en un point.
Il y a toujours deux possibilités de toucher en un ou deux points, il faut trouver la bonne. Par exemple avec les valeurs par défaut de la feuille de calcul, on a le choix entre 42645 et -6883. Faites l'essai !
C'est seulement lorsque le minimum est trouvé que l'on peut lire les résultats suivant.

Le deuxième résultat permet de vérifier le critère de Rayleigh.
Le critère de Rayleigh stipule que pour que deux étoiles soient distinctes à l'oeil il faut au moins qu'elles soient écartées d'un rayon d'Airy. Pour cela :
Le plus grand défaut sur l'onde ne doit pas dépasser le quart de la longueur d'onde. On parle de lambda sur quatre: L / 4
Attention: Le critère de Rayleigh n'a pas de sens si le critère de Couder n'est pas satisfait au préalable: Car avant de voir si deux images de diffractions sont distinctes, il faut qu'il y ait des images de diffraction...
Le troisième résultat permet de savoir où travailler le verre.
Le troisième résultat n'est intéressant que lorsque l'on travaille un miroir en fabrication. Il indique le profil du verre à enlever et les zones à travailler pour améliorer le miroir.

Enfin il est possible d'améliorer la présentation des résultats une fois le lambda trouvé.
La feuille de calcul donne la valeur de la « Constante pour la meilleure onde ». Que l'on peut recopier manuellement dans la case « Valeur retenue ». La valeur de l' « Écart de focale » est alors nulle et les profils de la meilleure onde sont plats.
![]()
Ceci est possible car la constante de la meilleure onde n'est que la traduction de l'imperfection du choix de la constante.
La constante n'étant que la transcription de la méconnaissance de la position exacte (au micron) du meilleur foyer du miroir.
Enfin cet aplatissement des meilleures ondes permet de bien comprendre que leur forme parabolique, qu'elles ont, lorsque la constante n'est pas parfaite, n'est qu'un artéfact de calcul sans aucune relation avec la forme exacte de l'onde.
La copie d'écran ci-dessous montre comment opère la nouvelle constante.
Formules – Symboles - Unités
Diamètre du miroir en mm ( Diamètre : D )
Longueur d'onde: usuellement 560 nm, mais certains prennent 550 nm.
Focale du miroir en mm ( Focale : R/2 )
R est le rayon de courbure du miroir. Il est égal au double de la focale du miroir.
Rayon d'Airy en micron ( RA = 1,22x Longueur d'onde/1000 x Focale/Diamètre)
Limites des zones en mm ( hx )
Hauteur médiane de la zone en mm ( hm )
Aberration longitudinale de stigmatisme en mm ( hm²/R )
Mesures en mm ( Mn )
Constante pour centrer les mesures en mm ( c = voir formule dans la feuille de calcul)
Mesures centrées en mm ( Mn – c )
Aberration longitudinale résiduelle en mm ( ALR = Mn-c – hm²/R )
Aberration transverse au foyer en µm ( ATF = 1000 x ALR x hm / 2R )
Aberration transverse réduite ( ATF / RA )
Pente sur l'onde [ nm / mm ] ( -1000 x ATF / (R/2) )
Profil de l'onde [ nm ] ( intégrale de la pente depuis le centre du miroir)
Écart de focale [ nm ]( valeur à saisir pour minimiser l'écart Pic-Vallée )
Calcul intermédiaire ( voir formule dans la feuille de calcul )
Écart Pic-Vallée en nanomètre sur l'onde ( voir formule dans la feuille de calcul )
Écart Pic-Vallée en fraction d'onde ( Longueur d'onde / Écart Pic-Vallée )
Meilleure onde dessus en nm ( voir formule dans la feuille de calcul )
Meilleure onde dessous en nm ( voir formule dans la feuille de calcul )
Verre à enlever [ nm ] ( (Profil de l'onde - Meilleure onde dessous)/2 )
Constante pour la meilleure onde en mm ( c = constante retenue – 4 x Écart de focale x 1000000)